Као што СциПи је отворени извор, има веома активну и живахну заједницу програмера због чега постоји огроман број модула за велику количину научних апликација и прорачуна доступних са СциПи. Неке од сложених математичких операција које се могу извести са СциПи су:
- Интерполација
- Интеграција
- Оптимизација
- Обрађиванње слике
- Статистика
- Прорачуни за посебне функције итд.
СциПи се може упоредити са већином командних и стандардних библиотека попут ГСЛ библиотеке за Ц ++ и Матлаб. Како је СциПи изграђен на врху НумПи пакета, ова два пакета такође могу бити потпуно интегрисана. Ако можете да смислите математичку операцију коју треба обавити, обавезно проверите СциПи библиотеку пре него што самостално имплементирате тај модул, јер у већини случајева СциПи већ има све операције за вас.
Инсталирајте СциПи Либрари
Инсталирајмо СциПи библиотеку пре него што пређемо на стварне примере и концепте. Постоје два начина за инсталирање овог пакета. Први укључује употребу Питхон менаџера пакета, пип:
пип инсталл сципиДруги начин се односи на Анацонду, пакет можемо инсталирати као:
цонда инсталл -ц анацонда сципиЈедном када је библиотека инсталирана, можемо је увести као:
импорт сципиКоначно, како ћемо користити и НумПи (препоручује се да за све НумПи операције користимо НумПи директно, уместо да пролазимо кроз СциПи пакет):
импорт нумпиМогуће је да ћемо у неким случајевима такође желети да зацртамо своје резултате за које ћемо користити Матплотлиб библиотеку. Извршите следећи увоз за ту библиотеку:
импорт матплотлибКористићу менаџер Анацонде за све примере у овој лекцији. Покренућу Јупитер Нотебоок за исти:

Сад кад смо спремни да са свим наредбама за увоз напишемо неки код, почнимо да зарањамо у СциПи пакет са неколико практичних примера.
Рад са полиномским једначинама
Започећемо са разматрањем једноставних полиномских једначина. Постоје два начина на која можемо интегрисати полиномске функције у наш програм. Можемо искористити поли1д класа која користи коефицијенте или корене полинома за иницијализацију полинома. Погледајмо пример:
из нумпи импорт поли1дфирст_полиномиал = поли1д ([3, 4, 7])
испис (први_полином)
Када покренемо овај пример, видећемо следећи излаз:

Јасно је да је полиномни приказ једначине одштампан као излаз, тако да је резултат прилично лако разумљив. Можемо изводити разне операције и на овом полиному, попут квадрата, пронаћи његов дериват или га чак решити за вредност к. Покушајмо да урадимо све ово у следећем примеру:
принт ("Полиномски квадрат: \ н")испис (први_полином * први_полином)
принт ("Дериват полинома: \ н")
принт (први_полином.дерив ())
принт ("Решавање полинома: \ н")
испис (први_полином (3))
Када покренемо овај пример, видећемо следећи излаз:
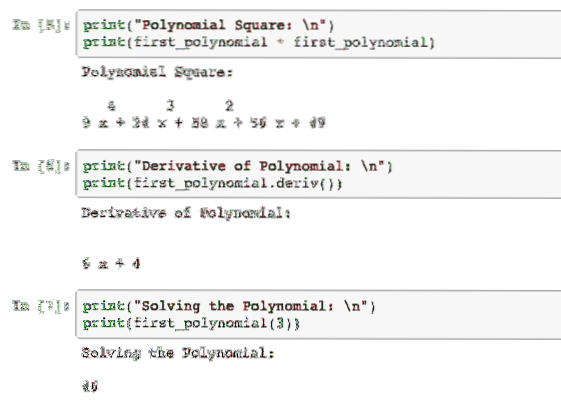
Таман кад сам размишљао да је ово све што можемо учинити са СциПи-ом, сетио сам се да можемо интегрисати и полином. Извршимо последњи пример са Полиномима:
принт ("Интегрисање полинома: \ н")принт (први_полином.интег (1))
Цео број који проследимо говори пакету колико пута да интегрише полином:
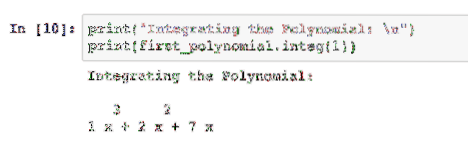
Једноставно можемо додати још један цео број који пакету говори колико пута треба интегрисати овај полином.
Решавање линеарних једначина
Могуће је чак и помоћу СциПи-а решити линеарне једначине и пронаћи њихове корене ако постоје. Да бисмо решили линеарне једначине, представљамо скуп једначина као НумПи низове и њихово решење као засебне НумПи низове. Визуелизујмо то на примеру где радимо исто и користимо се линалг пакет за проналажење корена једначина, ево једначина које ћемо решавати:
1к + 5и = 63к + 7и = 9
Решимо горње једначине:
од сципи импорт линалгједначина = нп.низ ([[1, 5], [3, 7]])
решење = нп.низ ([[6], [9]])
корени = линалг.решити (једначина, решење)
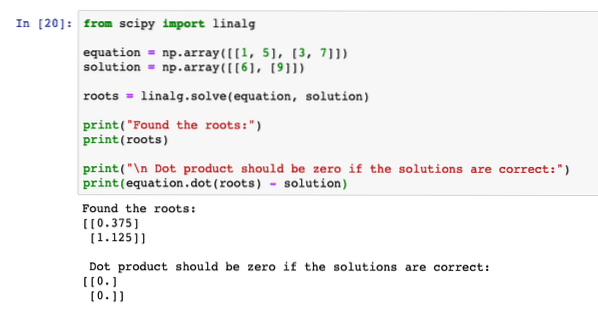
принт ("Пронашли корене:")
принт (корени)
принт ("\ н Тачкасти производ треба да буде нула ако су решења тачна:")
испис (једначина.тачка (корени) - решење)
Када покренемо горњи програм, видећемо да једначина тачканог производа даје нулти резултат, што значи да су корени које је програм пронашао били тачни:
Фуријеове трансформације са СциПи
Фуријеове трансформације помажу нам да изразимо функцију као одвојене компоненте које чине ту функцију и води нас кроз начин на који можемо рекомбиновати те компоненте да бисмо вратили оригиналну функцију.
Погледајмо једноставан пример Фуријеових трансформација где цртамо суму два косинуса користећи Матплотлиб библиотеку:
од сципи.ффтпацк увоз ффт# Број тачака узорка
Н = 500
# размак узорка
Т = 1.0/800.0
к = нп.линспаце (0.0, Н * Т, Н)
и = нп.цос (50.0 * 2.0 * нп.пи * к) + 0.5 * нп.јер (80.0 * 2.0 * нп.пи * к)
иф = ффт (и)
кф = нп.линспаце (0.0, 1.0 / (2.0 * Т), Н // 2)
# матплотлиб за сврхе цртања
импорт матплотлиб.пиплот као плт
плт.заплет (кф, 2.0 / Н * нп.абс (иф [0: Н // 2]))
плт.наслов ('Информације')
плт.илабел ('И оса')
плт.клабел ('Кс оса')
плт.грид ()
плт.Прикажи()
Овде смо започели конструисањем узорака простора и једначине косинуса које смо затим трансформисали и уцртали. Ево резултата горњег програма:
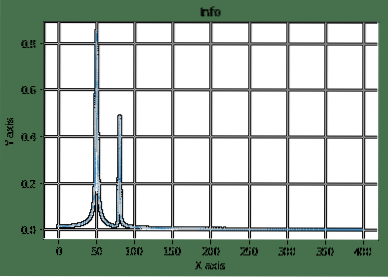
Ово је један од добрих примера где видимо да се СциПи користи у сложеној математичкој једначини за лаку визуализацију ствари.
Вектори и матрица са СциПи-јем
Сада када знамо пуно ствари за које је СциПи способан, можемо бити сигурни да СциПи може радити и са векторима и матрицом. Матрице су важан део линеарне алгебре јер су матрице нешто што користимо и за представљање векторских пресликавања.
Баш као што смо гледали на решавање линеарних једначина са СциПи, тако можемо представити векторе нп.арраи () функције. Почнимо са конструисањем матрице:
ми_матрик = нп.матрица (нп.случајни.насумично ((3, 3)))испис (ми_матрик)
Ево резултата горњег исечка:

Кад год говоримо о матрицама, увек говоримо о сопственим вредностима и сопственим векторима. Једноставније речено, сопствени вектори су вектори који, помножени матрицом, не мењају свој смер, за разлику од већине вектора. То значи да чак и када помножите сопствене векторе матрицом, постоји вредност (или сопствена вредност) која је један од фактора множења. Ово значи:
Ак = λк.У горњој једначини А је матрица, λ је сопствена вредност, а к вектор. Напишимо једноставан фрагмент кода да пронађемо сопствене вредности за дати Вектор:
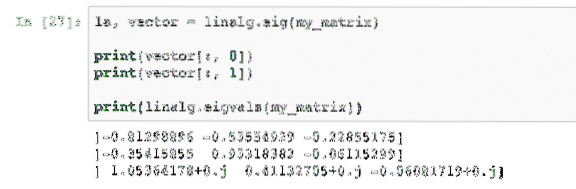
ла, вектор = линалг.еиг (ми_матрик)испис (вектор [:, 0])
испис (вектор [:, 1])
отисак (линалг.еигвалс (ми_матрик))
Када покренемо овај пример, видећемо следећи излаз:
Израчуната матрична одредница
Следећа операција коју ћемо извршити са СциПи је израчунавање одреднице дводимензионалне матрице. Поново ћемо користити матрицу коју смо користили у последњем исечку кода овде:
линалг.дет (ми_матрик)Када покренемо овај пример, видећемо следећи излаз:

Закључак
У овој лекцији смо погледали пуно добрих примера где нам СциПи може помоћи извођењем сложених математичких прорачуна за нас помоћу АПИ-ја и пакета који се лако користе.
 Phenquestions
Phenquestions