Код овог блога, заједно са скупом података, доступан је на следећој вези хттпс: // гитхуб.цом / схекхарпандеи89 / к-значи
К-Меанс кластерисање је ненадгледани алгоритам машинског учења. Ако упоредимо алгоритам К-Меанс ненадгледаног кластерирања са надгледаним алгоритмом, није потребно тренирати модел са означеним подацима. К-Меанс алгоритам се користи за класификацију или груписање различитих објеката на основу њихових атрибута или обележја у К број група. Овде је К цео број. К-Меанс израчунава удаљеност (користећи формулу растојања), а затим проналази минималну удаљеност између тачака података и центроид кластера за класификацију података.
Хајде да разумемо К-средства користећи мали пример користећи 4 објекта, а сваки објекат има 2 атрибута.
| ОбјецтсНаме | Атрибут_Кс | Атрибут_И |
|---|---|---|
| М1 | 1 | 1 |
| М2 | 2 | 1 |
| М3 | 4 | 3 |
| М4 | 5 | 4 |
К-Средства за решавање нумеричког примера:
Да бисмо решили горњи нумерички проблем путем К-Меанс-а, морамо следити следеће кораке:
К-Меанс алгоритам је врло једноставан. Прво морамо да изаберемо било који случајни број К, а затим да изаберемо центроиде или центар кластера. Да бисмо изабрали центроиде, можемо одабрати било који случајни број објеката за иницијализацију (зависи од вредности К).
Основни кораци алгоритма К-Меанс су следећи:
- Наставља да ради док се ниједан предмет не помери са својих центроида (стабилно).
- Прво изаберемо неке центроиде насумично.
- Затим одређујемо растојање између сваког објекта и центроида.
- Груписање предмета на основу минималне удаљености.
Дакле, сваки објекат има две тачке као Кс и И, а они на простору графикона представљају следеће:
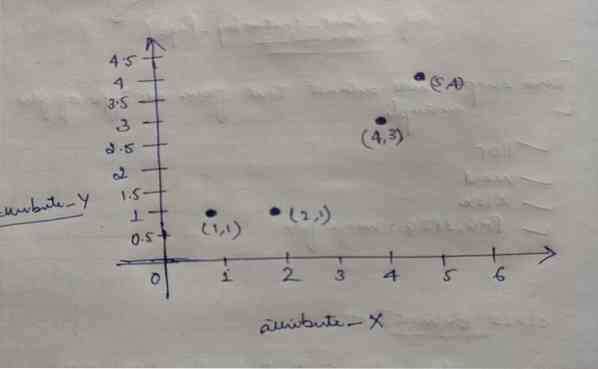
Дакле, у почетку бирамо вредност К = 2 као случајну да бисмо решили наш горњи проблем.
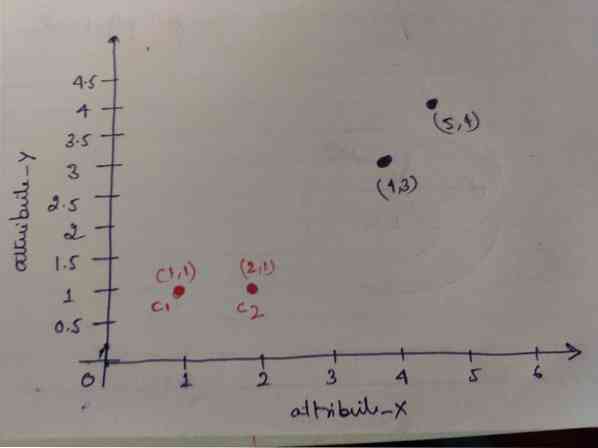
Корак 1: У почетку бирамо прва два објекта (1, 1) и (2, 1) као своје центроиде. Доњи графикон показује исто. Те центроиде називамо Ц1 (1, 1) и Ц2 (2,1). Овде можемо рећи да је Ц1 група_1, а Ц2 група_2.
Корак 2: Сада ћемо израчунати сваку тачку података објекта до центроида користећи еуклидску формулу растојања.
За израчунавање удаљености користимо следећу формулу.

Израчунавамо удаљеност од предмета до центроида, као што је приказано на доњој слици.

Дакле, израчунали смо удаљеност тачке података сваког објекта помоћу горе наведене методе растојања, коначно добили матрицу растојања као што је дато у наставку:
ДМ_0 =
| 0 | 1 | 3.61 | 5 | Ц1 = (1,1) цлустер1 | гроуп_1 |
| 1 | 0 | 2.83 | 4.24 | Ц2 = (2,1) цлустер2 | гроуп_2 |
| А | Б | Ц | Д | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | Икс |
| 1 | 1 | 3 | 4 | И |
Сада смо израчунали вредност удаљености сваког објекта за сваки центроид. На пример, објектне тачке (1,1) имају вредност растојања до ц1 је 0 и ц2 је 1.
Како из горње матрице растојања сазнајемо да објект (1, 1) има растојање до кластера1 (ц1) је 0, а до кластера2 (ц2) је 1. Дакле, објект један је близу самог кластера1.
Слично томе, ако проверимо објекат (4, 3), удаљеност до кластера 1 је 3.61 и кластеру 2 је 2.83. Дакле, објекат (4, 3) ће се пребацити у кластер2.
Слично томе, ако потражите објекат (2, 1), удаљеност до кластера 1 је 1, а до кластера 2 0. Дакле, овај објекат ће се пребацити на цлустер2.
Сада, према њиховој вредности удаљености, групишемо тачке (груписање објеката).
Г_0 =
| А | Б | Ц | Д | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | гроуп_1 |
| 0 | 1 | 1 | 1 | гроуп_2 |
Сада, према њиховој вредности удаљености, групишемо тачке (груписање објеката).
И на крају, графикон ће изгледати доле након груписања (Г_0).
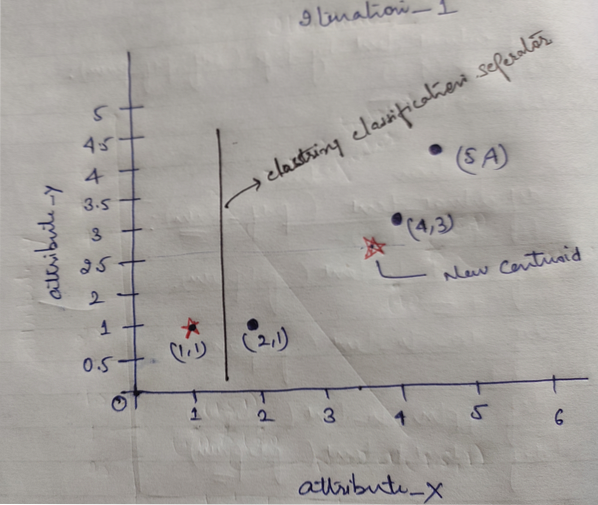
Понављање_1: Сада ћемо израчунати нове центроиде како су се почетне групе мењале због формуле растојања као што је приказано у Г_0. Дакле, гроуп_1 има само један објекат, тако да је његова вредност и даље ц1 (1,1), али гроуп_2 има 3 објекта, тако да је њена нова центроид вредност 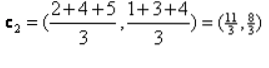
Дакле, нови ц1 (1,1) и ц2 (3.66, 2.66)
Сада опет морамо израчунати сву удаљеност до нових центроида као што смо рачунали раније.
ДМ_1 =
| 0 | 1 | 3.61 | 5 | Ц1 = (1,1) цлустер1 | гроуп_1 |
| 3.14 | 2.36 | 0.47 | 1.89 | Ц2 = (3.66,2.66) цлустер2 | гроуп_2 |
| А | Б | Ц | Д | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | Икс |
| 1 | 1 | 3 | 4 | И |
Итератион_1 (груписање објеката): Сада, у име израчунавања нове матрице растојања (ДМ_1), групишемо је према томе. Дакле, премештамо објекат М2 из групе_2 у групу_1 као правило минималне удаљености до центроида, а остатак објекта биће исти. Тако ће ново груписање бити као испод.
Г_1 =
| А | Б | Ц | Д | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | гроуп_1 |
| 0 | 0 | 1 | 1 | гроуп_2 |
Сада морамо поново израчунати нове центроиде, јер оба објекта имају две вредности.
Дакле, нови центроиди ће бити 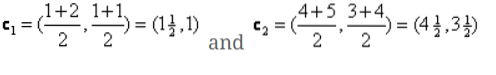
Дакле, након што добијемо нове центроиде, груписање ће изгледати доле:
ц1 = (1.5, 1)
ц2 = (4.5, 3.5)
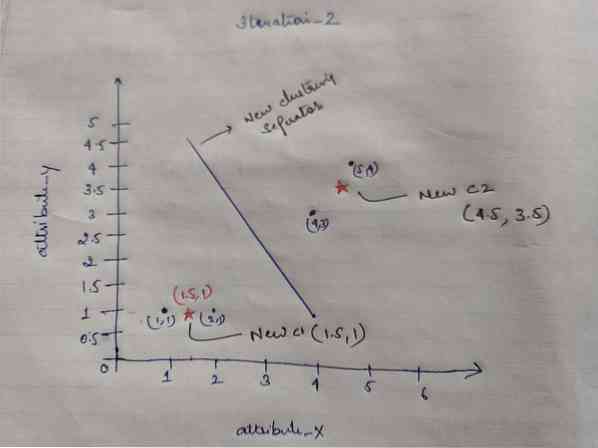
Понављање_2: Понављамо корак у којем израчунавамо нову удаљеност сваког објекта до нових израчунатих центроида. Дакле, након израчунавања, добићемо следећу матрицу растојања за итерацију_2.
ДМ_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | Ц1 = (1.5, 1) цлустер1 | гроуп_1 |
| 4.30 | 3.54 | 0.71 | 0.71 | Ц2 = (4.5, 3.5) цлустер2 | гроуп_2 |
А Б Ц Д
| А | Б | Ц | Д | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | Икс |
| 1 | 1 | 3 | 4 | И |
Опет, задатке груписања радимо на основу минималне удаљености као и пре. Дакле, након што смо то урадили, добили смо матрицу кластеровања која је иста као Г_1.
Г_2 =
| А | Б | Ц | Д | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | гроуп_1 |
| 0 | 0 | 1 | 1 | гроуп_2 |
Као овде, Г_2 == Г_1, тако да није потребна додатна итерација и овде можемо да се зауставимо.
К-Меанс Имплементатион користећи Питхон:
Сада ћемо применити алгоритам К-значи у питхон-у. Да бисмо применили К-средства, користићемо познати Ирис скуп података, који је отвореног кода. Овај скуп података има три различите класе. Овај скуп података у основи има четири карактеристике: Дужина залиска, ширина залиска, дужина латица и ширина латица. Последња колона ће рећи име класе тог реда попут сетоса.
Скуп података изгледа као у наставку:
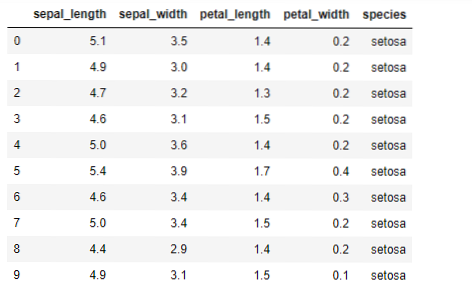
За имплементацију питхон к-значи, морамо да увеземо потребне библиотеке. Дакле, ми увозимо Панде, Нумпи, Матплотлиб, а такође и КМеанс из склеарна.гомила као што је дато у наставку:

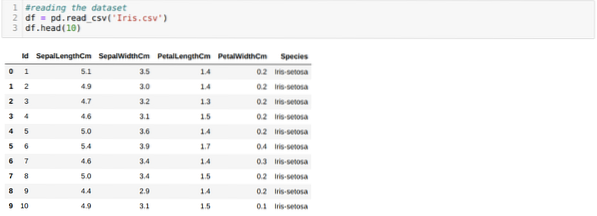
Читамо Ирис.цсв скуп података користећи методу реад_цсв панде и приказаће првих 10 резултата методом хеад.
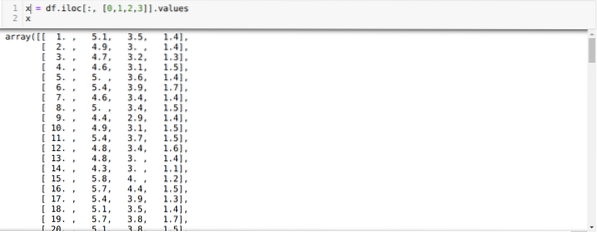
Сада читамо само оне карактеристике скупа података које су нам биле потребне за обуку модела. Дакле, читамо све четири карактеристике скупова података (дужина залиска, ширина залиска, дужина латица, ширина латица). Због тога смо пренели четири вредности индекса [0, 1, 2, 3] у илоц функцију оквира података панде (дф) као што је приказано доле:
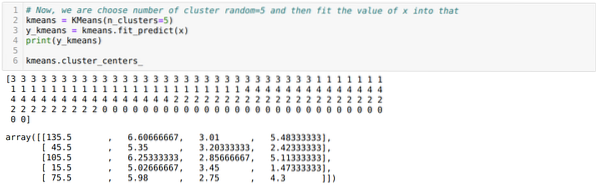
Сада насумце бирамо број кластера (К = 5). Креирамо објекат класе К-средства, а затим уклапамо свој к скуп података у онај за обуку и предвиђање као што је приказано доле:
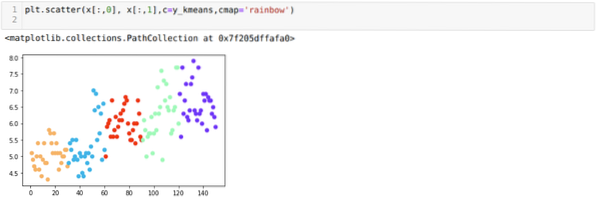
Сада ћемо визуализовати наш модел са случајном вредношћу К = 5. Јасно можемо видети пет кластера, али изгледа да то није тачно, као што је приказано доле.
Дакле, наш следећи корак је да откријемо да ли је број кластера био тачан или не. А за то користимо методу Лакат. Метода Елбов користи се за проналажење оптималног броја кластера за одређени скуп података. Овом методом ћемо утврдити да ли је вредност к = 5 била тачна или не, јер не добијамо јасно кластерисање. Дакле, након тога идемо на следећи графикон који показује да вредност К = 5 није тачна јер оптимална вредност пада између 3 или 4.
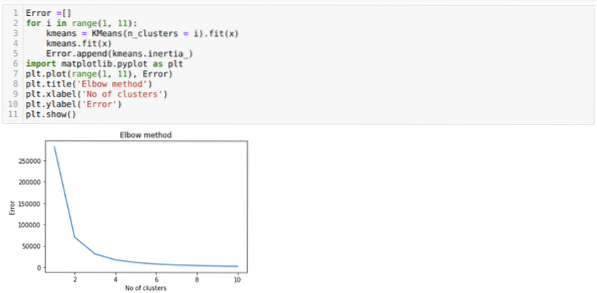
Сада ћемо поново покренути горњи код са бројем кластера К = 4, као што је приказано доле:
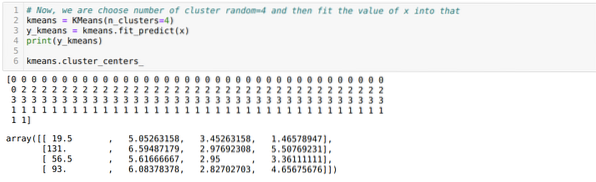
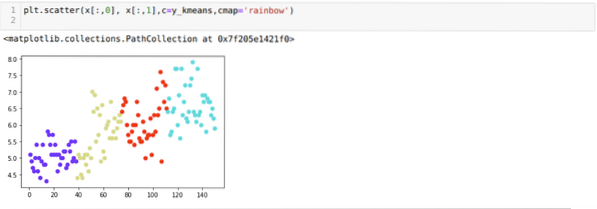
Сада ћемо визуализовати горње К = 4 кластер нове градње. Екран испод показује да се сада груписање врши помоћу к-средстава.
Закључак
Дакле, проучавали смо алгоритам К-средина и у нумеричком и у питхон коду. Такође смо видели како можемо сазнати број кластера за одређени скуп података. Понекад метода Лакат не може дати тачан број кластера, па у том случају постоји неколико метода које можемо изабрати.
 Phenquestions
Phenquestions